Fraunhofer Diffraction At A Single Slit

• Fraunhofer Diffraction At A Single Slit Time
• Fraunhofer Diffraction At A Single Slit Light
• Fraunhofer Diffraction Music
• Single Slit Fraunhofer Diffraction

Joseph Fraunhofer first used diffraction gratings in 1819 to observe the spectrum of the sun. Earliest devices were multiple-slit assemblies, consisting of a grid of fine wire or thread wound about and extending between two parallel screws, which served as spacers.

Explain Fraunhofer diffraction at a single slit with a neat ray diagram. Obtain an expression for the width of the central bright fringe.

Under the Fraunhofer conditions, the wave arrives at the single slit as a plane wave. Divided into segments, each of which can be regarded as a point source, the amplitudes of the segments will have a constant phase displacement from each other, and will form. Single slit diffraction term N slit interference term Note: For N=1, single slit diffraction intensity For N =2, double slit diffraction intensity Thus above expression of intensity is the most general one for any number of slits! 2 2 0 sin E E I I J E E 2 2 2 0 cos sin I I Dr. Kamalika Hajra 20. Fraunhofer Single Slit This is an attempt to more clearly visualize the nature of single slit diffraction. The phenomenon of diffractioninvolves the spreading out of waves past openings which are on the order of the wavelength of the wave. Link of ' fraunhoffer diffraction at a single slit part - 2 ' video.link of ' newton rings part - 1 ' video.

Solution

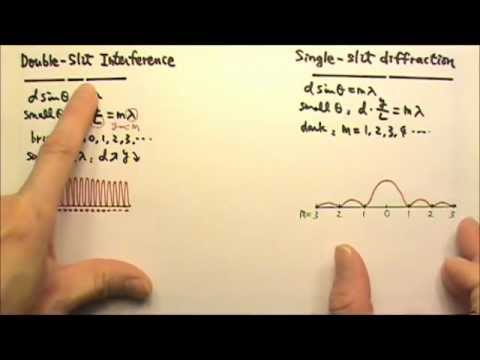
Fraunhofer diffraction due to single slit:

1. Consider a narrow slit AB of width ‘a', kept perpendicular to the plane of the paper. The slit can be imagined to be divided into extremely thin slits or slit elements. It is illuminated by a parallel beam of monochromatic light of wavelength λ i.e., a plane wavefront is an incident on AB.
2. The diffracted light is focused by a converging lens L, on a screen XY.
3. The screen is kept in the focal plane of the lens and is perpendicular to the plane of the paper.
4. Let D be the distance between the slit and the screen.
5. According to Huygens' principle, each and every point of the slit acts as a source of secondary wavelets, spreading in all directions.

Position of central maxima:

1. Let C be the centre of the slit AB. The secondary wavelets traveling parallel to CP_o come to a focus at P_o. The secondary wavelets from points equidistant from C in the upper and lower halves of the slit travel equal paths before reaching P_o.
2. The optical path difference between all these wavelets is zero and hence they interfere in the same phase forming a bright image at P_o.
3. The intensity of light is maximum at the point P_o. It is called the central or the principal maxima of the diffraction pattern.
4. For the line CP_o, angle θ = 0°.

Position of secondary minima:

1. Consider a point P on the screen at which waves travelling in a direction making an angle θ with CP are brought to focus at P by the lens. This point P will be of maximum or minimum intensity because the waves reaching P will cover the unequal distance.
2. Draw AN perpendicular to the direction of diffracted rays from point A. BN is the path difference between secondary waves coming from A and B.
3. From ΔABN, sin θ = `'BN'/'AB'`
   ∴ BN = AB sin θ = a sin θ
   Since θ is very small
   ∴ sin θ ≈ θ
   ∴ BN = aθ
   In figure, suppose BN = λ and θ = θ₁ then sin θ₁ = `lambda/'a'`
4. Such a point on the screen will be the position of the first secondary minimum. It is because, if the slit is assumed to be divided into two equal halves AC and BC, then the waves from corresponding points of two halves of the slit will have a path difference of λ/2.
   It gives rise to destructive interference at P which has minimum intensity.
5. If point P on the screen is such that BN = 2λ and angle θ = θ₂, then, sin θ₂ = `(2λ)/'a'`. Such a point on the screen will be the position of the second secondary minimum.
   In general, for n^th minimum, sinθ_n = `('n'lambda)/'a'`
   where, n = ±1, ±2, ±3,…
6. If y_nd is the distance of n^th minimum from P_o, on the screen, then `(tan theta_'nd') = ('y'_'nd')/'D'`.
7. If θ_nd is very small,
8. tan θ_nd ≈ sin θ_nd = `('n'lambda)/'a'`
9. ∴ `('y'_'nd')/'D' = ('n'lambda)/'a'`
10. ∴ `'y'_'nd' = ('n'lambda'D')/'a'` = nW ....(1)
    where, W is fringe width Equation (1) gives distance of n^th secondary minima from central maxima.
11. The central bright fringe is spread between the first dark fringes on either side. Hence, width of the central bright fringe is the distance between the centres of first dark fringe on either side.
    ∴ Width of the central bright fringe,
    W_c = 2y_1d = 2W = 2`((lambda'D')/'a')`
    This is the required expression for the width of the central bright fringe.

In a single slit diffraction pattern, the distance between first minima on the right and first minima on the left of central maximum is 4 mm. The screen on which the pattern is displaced, is 2m from the slit and wavelength of light used is 6000Å. Calculate width of the slit and width of the central maximum.

Solution

Given:- λ = 6000 Å = 6 x 10^-7 m,

D = 2 m,

X₁ + X₂ = 4 mm = 4 x 10^-3 m

To find:- Width of slit (a)

Width of central maximum (W)

Formula:-

i. `X_1+X_2=(2lambdaD)/a`

ii. W = X₁ + X₂

Fraunhofer Diffraction At A Single Slit Time

Calculation: From formula (i),

`4xx10^-3=(2xx6xx10^-7xx2)/a`

`therefore a=6xx10^4m`

The width of the slit is 6 x 10^-4 m.

From formula (ii),

Width of central maximum = 4 x 10^-3 m

Fraunhofer Diffraction At A Single Slit Light

The width of the central maximum is 4 x 10^-3 m.

Fraunhofer Diffraction Music

Video TutorialsVIEW ALL [2]

Single Slit Fraunhofer Diffraction

• 
  view
  Video Tutorials For All Subjects